Wir erinnern uns:
Bei den Verteidigungsrückzügern (VRZ) nehmen Weiß und Schwarz abwechselnd (selbstverständlich legale!) Züge zurück, wobei Weiß versucht, das anschließende “Vorwärts-Ziel”, meist ein Matt in einem Zug, zu erreichen, Schwarz dies aber durch geeignete Zugrücknahmen zu verhindern sucht.
Beim Typ Proca entscheidet die zurücknehmende Partei über mögliche Entschläge, beim Typ Høeg die andere.
So ist es hier im Lexikon definiert -– eigentlich eine einfache Sache.
Beide Arten der Verteidigungsrückzüger sind quasi gleichzeitig und unabhängig voneinander erfunden worden, nämlich Ende des Jahres 1923.
Die Definitionen der beiden Typen unterscheiden sich nur in einem einzigen Punkt. Dieser Unterschied führt jedoch zu ziemlich unterschiedlichen Strategien: Während beim Proca-VRZ jede Partei einen kompletten Zug zurücknimmt, schaut das beim Typ Høeg anders aus: Die am Zug befindliche Partei bestimmt nur den eigenen Stein, dessen Zug zurück gespielt werden soll, sowie dessen ursprüngliches Standfeld. Damit ist der Zug aber noch nicht abgeschlossen; dies erfolgt erst durch die Entscheidungen der Gegenseite!
Nun nämlich bestimmt die Gegenpartei (natürlich im Rahmen der Legalität der entstehenden Stellungen), ob diese Zugbewegung einen Schlagfall einschließen konnte oder gar musste. Beantwortet sich diese Frage mit JA, so entscheidet diese Partei, also die Gegenseite, welcher Stein seiner Farbe entschlagen wird. Falls kein Stein aus retroanalytischen Gründen entschlagen werden muss, sondern entschlagen werden kann, so kann sie sich auch entscheiden, keinen Stein einzusetzen.
Diesen Unterschied wollen wir uns anhand des Schemas anschauen, mit dem Niels Høeg seine Idee ursprünglich vorgestellt hat -– das Gedankenspiel, das wir nun vornehmen werden, stammt selbstverständlich nicht von ihm, da er den Typ Proca noch nicht kannte.

Niels Høeg
Eskilstuna-Kuriren 1418, 8.12.1923
-1 & #1,VRZ Høeg (4+3)
Weiß könnte sofort mattsetzen: mit 1.Lg5#, aber auch mit 1.Sf7#. Aber er muss ja zunächst einen Zug zurücknehmen, der natürlich unschädlich sein soll, also weiterhin eines der Satzmatts erhalten soll. Ein beliebiger Springer-Rückzug (z.B. R 1.Sb7-d8) würde Schwarz erlauben, auf d8 einen eigenen Läufer oder eine Dame einzusetzen, und Weiß kann nicht mattsetzen.
Nun erscheint etwa R 1.Le7-h4 ganz pfiffig, denn das behält doch beide Mattdrohungen aufrecht! Aber auch dagegen kann sich Schwarz verteidigen, indem er auf h4 nun einen schwarzen Turm oder eine schwarze Dame ergänzt, und Weiß muss sich nun in seinem Vorwärtszug um die Abwehr dieses Schachgebots kümmern, kann also nicht mattsetzen!
Also bleibt Weiß nur, eine Umwandlung in den Springer zurückzunehmen: R Bd7-d8=S (Schwarz kann nichts einsetzen, da dieser Zug garantiert schlagfrei gewesen ist) würde funktionieren, aber scheitert am Retropatt. R Bc7-d8=S ist im Prinzip wie die Rücknahme eines Springerzuges, Schwarz kann auf d8 also einen Läufer oder eine Dame ergänzen. Also löst nur R Be7-d8=S, und nun kann Schwarz eine beliebige eigene Figur auf d8 einsetzen: Keine verteidigt, so dass Weiß nun mit Lg5 mattsetzen kann.
Interpretiert man die Stellung als VRZ Proca, so könnte Weiß alle möglichen Rückzüge auch zurücknehmen und entweder nichts oder Unschädliches entschlagen, z.B. R Sb7-d8 oder auch R Le7:Sh4 (Entschlag ist erforderlich, da Schwarz sonst retropatt wäre).
Da sieht man schon deutliche Unterschiede!
Schauen wir uns nun die erste „richtige“ VRZ Høeg Aufgabe an:
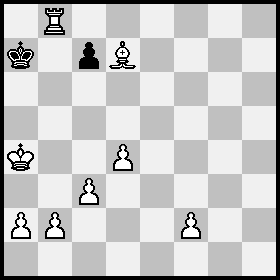
Niels Høeg
Eskilstuna-Kuriren 1419, 8.12.1923
-2 & #1,VRZ Høeg (8+2)
Weiß nimmt die Turmumwandlung auf b8 zurück: Damit kann Schwarz nichts entschlagen bzw. einsetzen und hat nun genau vier Felder, von denen sein König in seinem letzten Zug kommen konnte.
Kam der schwarze König von a8, so ergänzt Weiß auf a7 einen weißen Läufer, nimmt b6-b7+ zurück und setzt mit Lc6 matt. (Übrigens kann Weiß nicht wBa7 ergänzen: Das wäre legal, aber dann kann er nicht mit b6-b7 das Schach aufheben (sondern nur mit c6xXb7+), da dies zu einer illegalen Bauernstellung führen würde!)
Wie notiert man nun die Lösung? Nun, das kann man machen wie bei allen anderen Retro-Aufgaben auch, also für diese Variante R 1.b7-b8=T Ka8:La7 2.b6-b7+ & vor: 1.Lc6#.
Aber Niels Høeg hatte eine andere Schreibweise vorgesehen und sie in seiner Schrift On Retraction Chess Problems (1927) so eingeführt: „The moves of retraction chess are written down in the form in which the reversed move of ordinary chess would have been written, and added men are stated in [].”
Er hat also bewusst eine abweichende Notation gegenüber der üblichen Retro-Notation, die auch damals schon verbreitet war, gewählt. Der Grund erscheint mir sehr gut und überzeugend: Während beim normalen Retro (und auch beim Proca-VRZ) der komplette Zug vollständig von der zurücknehmenden Partei bestimmt wird (wie im Partieschach), weicht der Høeg-Typ ja hiervon ab. Die zurücknehmende Seite bestimmt ja nur Ausgangs- und Zielfeld ihrer Rücknahme, aber damit ist der Zug ja noch nicht abgeschlossen, sondern dann entscheidet die andere Seite, ob und wenn ja was entschlagen worden sein soll.
Ich schlage allerdings runde Klammern vor, um bei möglichen (Anti-) Circe Aufgaben nicht mit den eckigen Klammern zu kollidieren, die dort ja das Versetzungsfeld angeben.
Damit können dann alle vier Varianten angegeben werden:
R 1.b7-b8=T Ka8-a7(L) 2.b6-b7+ & vor: 1.Lc6#; 1.– Kb8-a7(T) 2.Lc6-d7(beliebig) & vor: 1.Ta8#; 1.– Ka6-a7(L) 2.b6-b7 & vor: Lc8#; 1.—Kb6-a7(T) 2.c2-c3 (einziger neutraler Wartezug!) & vor: 1.b8=D#.
Schaut euch noch einmal genau an, weshalb andere Einsetzungen nicht gehen!
Auch wenn die Høeg-Retraktoren längst nicht so verbreitet sind wie ihre Kollegen vom Proca-Typ, so bin ich fest davon überzeugt, dass hier noch jede Menge zu entdecken ist –- auf dem orthodoxen Gebiet ebenso wie zusammen mit Märchenbedingungen!
