Schlagwort-Archive: Rochade

Retro der Woche 14/2013

Veröffentlicht am von
Antworten

Zunächst einmal wünsche ich euch ein frohes Osterfest! Und wenn ihr nun die Ostereier im Garten unter den Schneebergen gefunden habt, freut ihr euch vielleicht, im Warmen sitzend bei einem Glas Glühwein das neue Retro der Woche anschauen und lösen zu können?!

Im heutigen Retro der Woche verbirgt sich auch ein Osterei: e2 ist nämlich ein “magisches Feld”: Diese Erfindung von Albert H. Kniest ist ganz einfach erklärt: Betritt ein Stein (außer einem König) ein magisches Feld, ändert er seine Farbe. Das kann schon im Vorwärtsspiel zu interessanten Strategien und Lösungen führen, aber besonders interessant finde ich es in Retro-Aufgaben.

Günther Weeth hatte die magischen Felder speziell im Zusammenhang mit Anticirce-Procas (siehe zum Beispiel das Retro der Woche 11/2013) wieder belebt, nachdem sie eine Weile nicht so häufig genutzt worden waren, und so lag es nahe, im von feenschach ausgeschriebenen Turnier zur Feier seines 75. Geburtstages magische Felder zu fordern.

Aus dem Preisbericht, der im Heft 194 (Juli-August 2012) erschienen ist, möchte ich hier den 2. Preis vorstellen.

Dirk Borst
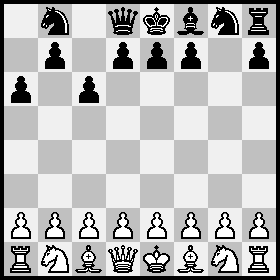
63. feenschach Thematurnier 2012, 2. Preis
Stellung nach dem 23. Zug (16+13); magisches Feld e2

Die Fragen, die der Autor dazu stellt, sind:

  1. Wurde der schwarze Turm a8 geschlagen?
  2. Welche Rochaderechte haben Weiß und Schwarz noch?

Irgendwelche Abzähl-Versuche der schwarzen oder weißen Züge sind zwecklos — welchen Ansatz für eine Antwort auf die Fragen könnten wir finden? Doch, den wesentlichen Hinweis gibt die Zügezahl! Weiß hat eine ungerade Anzahl von Zügen gemacht — das aber geht in der Partieausgangsstellung doch gar nicht?! Doch: Das geht hier wegen des magischen Feldes! Das bedeutet also, dass der weiße E-Bauer gezogen haben muss, dass also ein ehemals schwarzer Bauer nun auf e2 steht. Und das ist dann offensichtlich der sB von g7; ein anderer kommt nicht in Frage. Wen aber hat er (neben dem weißen e-Bauern) geschlagen?
Weiterlesen →

Retro der Woche 1/2013

Veröffentlicht am von
2

Das Retro der Woche 1/2013 erscheint schon im Jahr 2012 — macht der Retroblogger nun den verrückten Ehrgeiz vieler Zeitschriften-Herausgeber mit, möglichst früh da zu sein, das Januarheft Ende November, spätestens Anfang Dezember erscheinen zu lassen? (Gut, dass von diesem Bazillus Die Schwalbe und feenschach nicht befallen sind…)

Nein, wir wollen ja mit dem Retro der Woche in die neue Woche starten, und daher richte ich mich nach der Kalenderwochen-Zählung der kommenden Woche, und die orientiert sich bekanntlich am Donnerstag.

Zum Ende des Jahres möchte ich gern die Diskussion zum Ende der Beweispartie aufgreifen, die Bernd Gräfrath mit seinem Vortrag beim Schwalbetreffen in Göttingen (siehe 252 Die Schwalbe Dez. 2011, S.343ff und 254 Die Schwalbe Apr. 2012, S.439ff) angeregt hat und dabei nicht, wie wir es schon oft beim #2 und dem Hilfsmatt erlebt haben, über das “Ende durch Ausschöpfung” einer Gattung schwadroniert, sondern die wichtige ästhetische Frage stellt, wie wir es mit dem “Ankleben” von weiteren Zügen halten, nachdem das eigentliche Thema dargestellt ist.

Für mich ist das auch eine Frage der Ökonomie; dieser Begriff bedeutet für mich mehr als reines Steine-Zählen, sondern auch z.B. die Frage der Zeit-Ökonomie. Aber die Ökonomie ist für mich kein absoluter Wert, sondern muss immer im Kontext der konkreten Aufgabe und ihrer Darstellung gesehen werden. Da halte ich es mit Herbert Grasemann: “Ökonomisieren heißt Haare schneiden, nicht skalpieren.”

Thomas Brand
Probleemblad 2004 (nach E. Dupuis)
Beweispartie in 16 Zügen (14+13) Co+

Ich stand bei der heutigen Aufgabe auch vor der Frage, noch ein Zugpaar “anzukleben”, obgleich das eigentliche Thema schon nach 15 Zügen dargestellt ist. Allzu schwer sollte das Stück nicht zu lösen sein, wenn man darüber nachgedacht hat, wie fehlende Steine verschwinden konnten.
Weiterlesen →